Wie baut man eine negative Induktivität ?

.

• jump to ==> English version

.

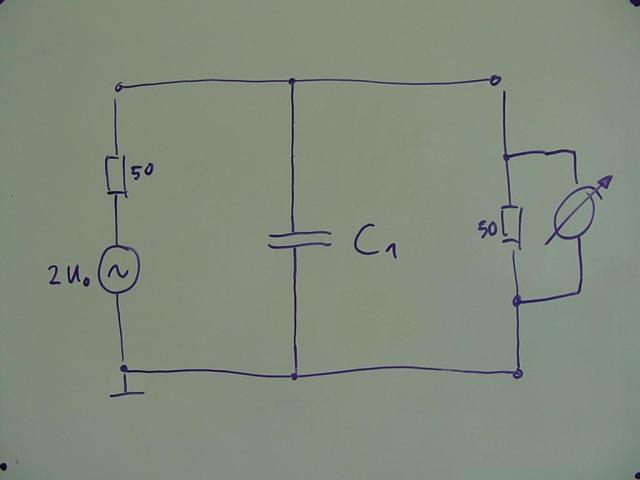
Hier haben wir einen typischen Filterkondensator in einer Meßanordnung

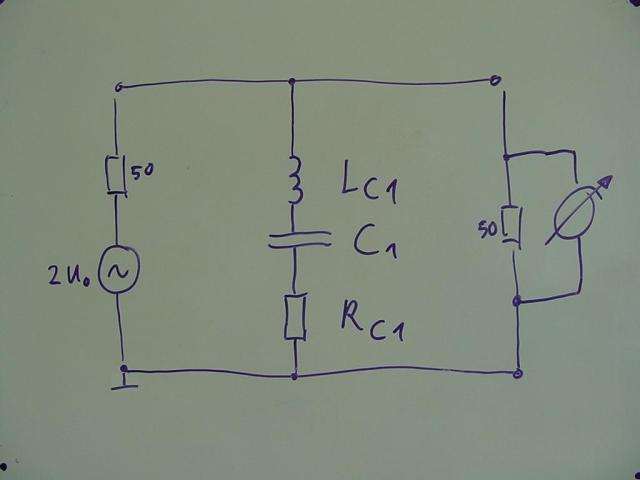
In der Realität besitzt jeder Kondensator eine parasitäre Induktivität und einen reellen Widerstand in Serie,

hier mit Lc1 und Rc1 bezeichnet (= ESL und ESR im Datenblatt)

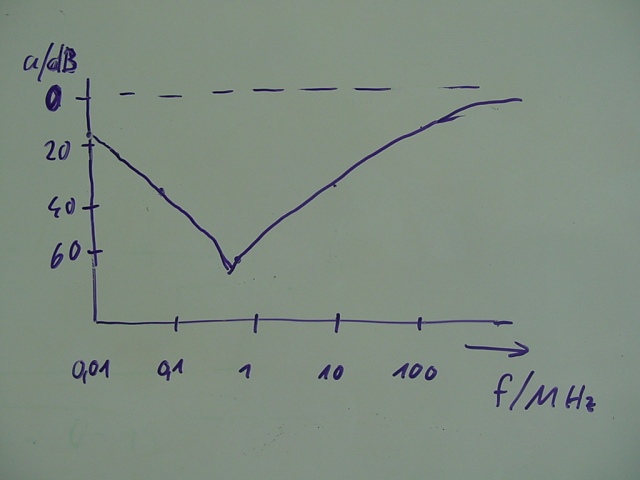
die den bekannten Frequenzverlauf ergeben

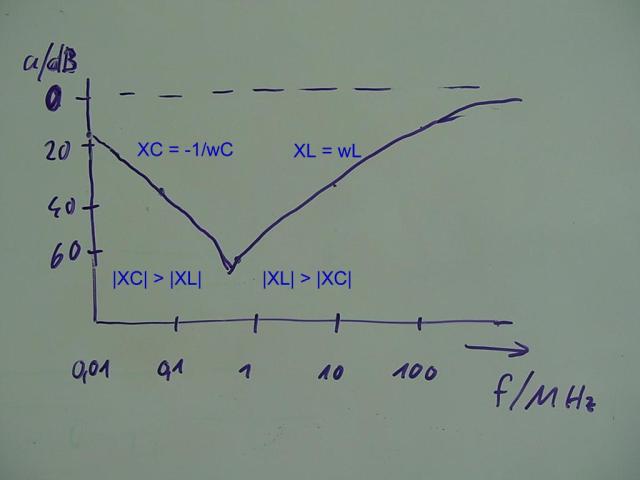
Für niedrige Frequenzen dominiert der Blindwiderstand des Kondensators – aber oberhalb der Resonanzfrequenz

wirkt sich die parasitäre Serien-Induktivität extrem störend aus:

Bei höheren Frequenzen (z.B. UKW) ist praktisch keine Wirkung mehr vorhanden

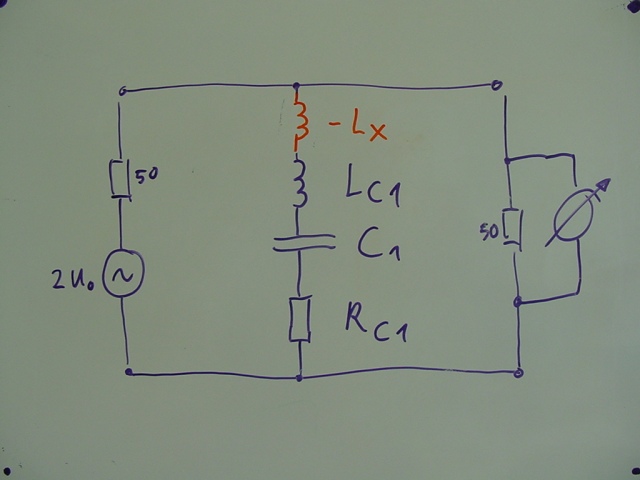
Wenn man eine negative Induktivität hätte , die genauso groß ist, wie die parasitäre,

könnte man sie einfach in Serie zu der störenden parasitären Induktivität des Kondensators schalten –

und beide würden sich gegenseitig aufheben (Lc1 – Lx = O ) und zwar frequenzunabhängig

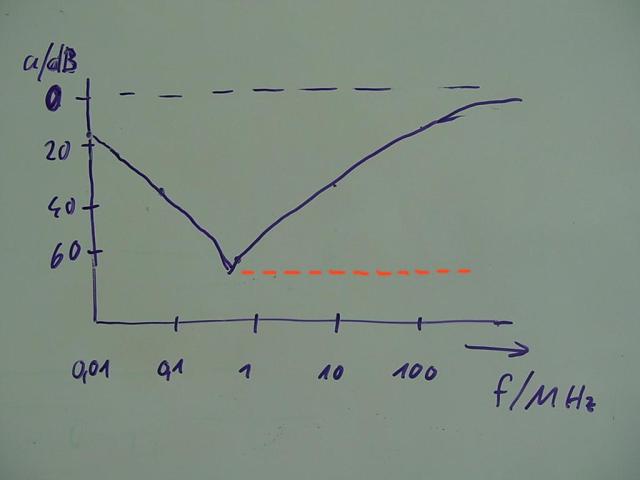
Dann würde die Filterwirkung oberhalb der Resonanz nicht abfallen, sondern

trotz steigender Frequenz konstant bleiben – wie in der orange gestrichelten Linie

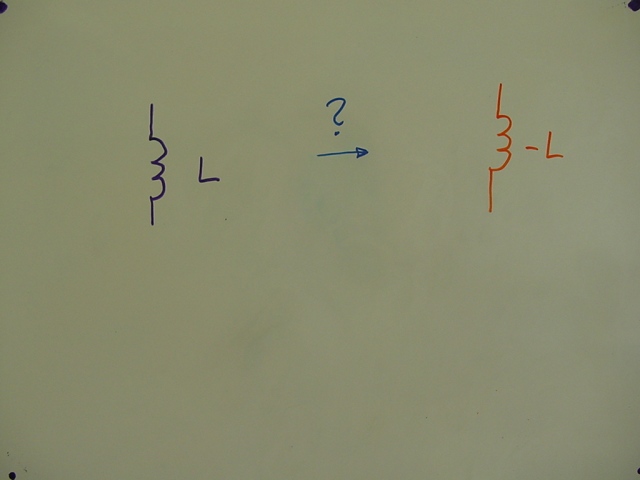
Nur – wie kommt man zu einer negativen Induktivität ?

Zunächst mal ist das ein unlösbares Problem:

passive, absolute, negative Bauteile können nicht so ohne weiteres realisiert werden, weil sie gegen den

Energierhaltungssatz verstoßen würden. Negative Bauteile verbrauchen keine Energie – sondern setzten

aus sich heraus Energie frei.

Anders ausgedrückt – mit negativen Bauteilen könnte man ein Perpetuum Mobile betreiben.

Es stellt sich also die Frage:

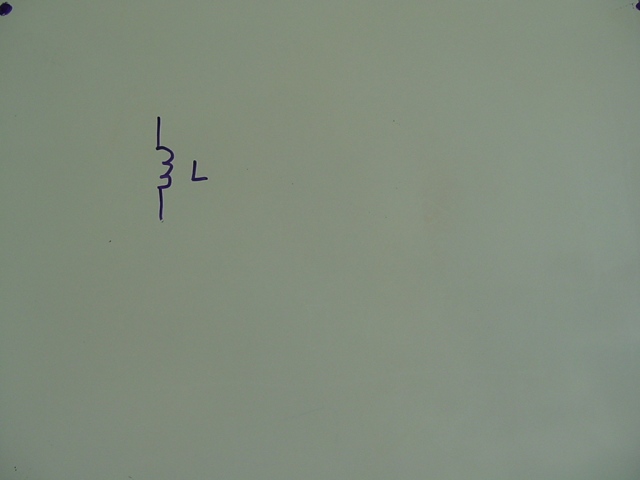
Man nimmt eine ganz normale Induktivität

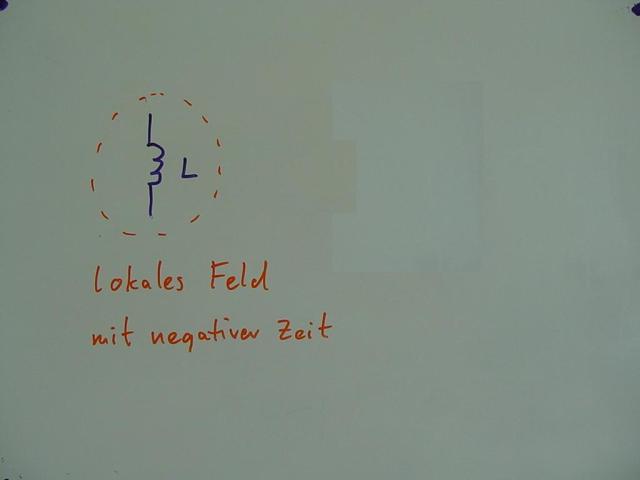
und gibt sie in ein lokales Feld mit negativer Zeit

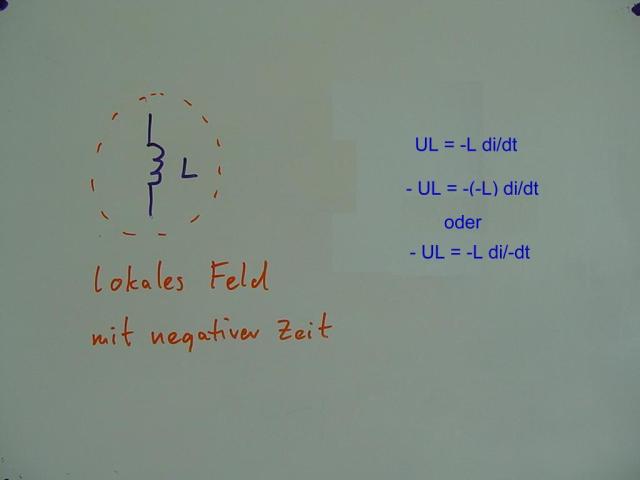
Die Spannung an der Induktivität L ist proportional zur Stromänderung di/dt in der Spule

Um eine umgekehrte Spannung an der Spule zu erzeugen, braucht man entweder eine Spule mit negativem L,

oder ein Stromänderung in negativer Zeitrichtung : di/-dt

Dann ergibt sich eine Spannung entgegengesetzt zur normalen Richtung.

Bloß – wie erzeugt man ein Feld mit negativer Zeit ?

Richtig – wir verwenden eine Zeitmaschine !

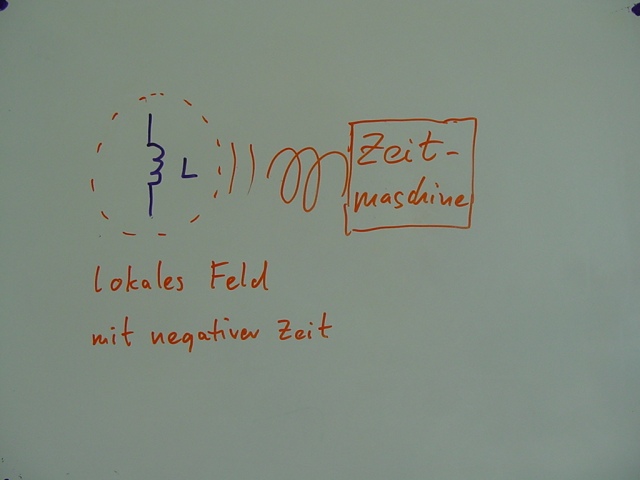
Bei einer Zeitreise in die Vergangenheit ist der Zeitablauf negativ – die Uhr läuft rückwärts –

im Wirkungsbereich der Zeitmaschine entsteht genau das benötigte lokale Feld mit negativer Zeit !

Tja – das Problem hätten wir gelöst – fehlt nur noch die Zeitmaschine !

Sehen wir uns mal die bekannten Zeitmaschinen an:

Einer der ersten Versionen findet sich im Film “The Time Machine”

Hübsch anzusehen – aber für unsere Zwecke definitiv zu viel Mechanik

Und hier ?

Der Flux-Kompensator !

Werden 2 Flux-Elemente durch positive Flux-Felder angeregt….

… so entsteht am 3. Element das negative Flux-Feld – das die negative Zeit erzeugt !

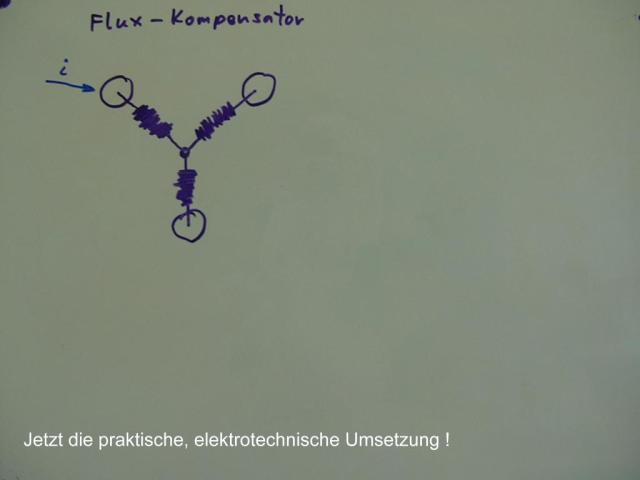
Wir leiten den Strom i in einen der Anschlüsse des Flux-Kompensators

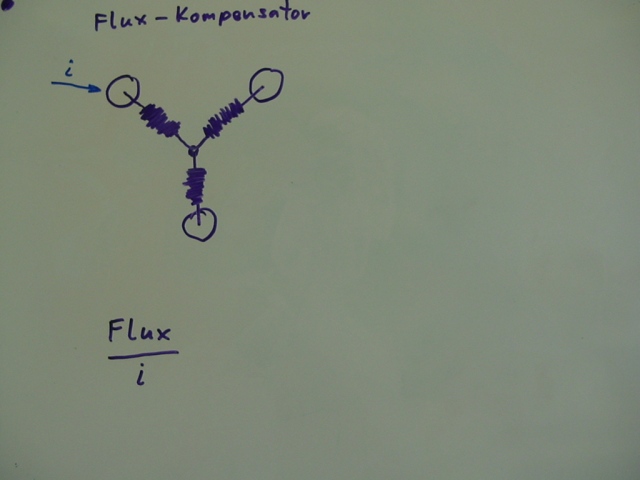
In dem Element entsteht Flux durch den Stromfluß – also Flux / i

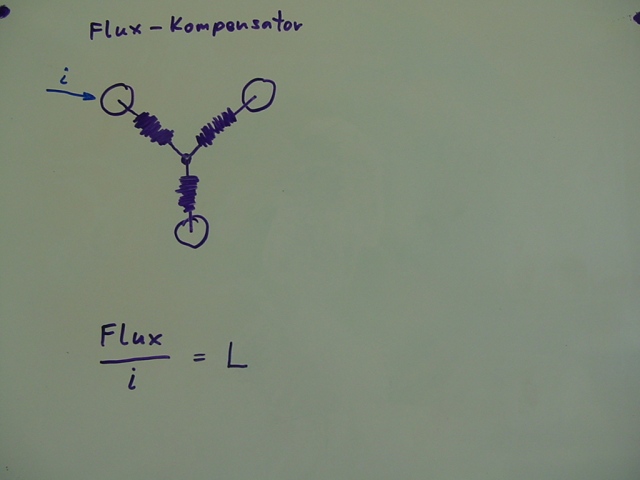
Das Verhältnis von erzeugtem Flux pro i definieren wir als L

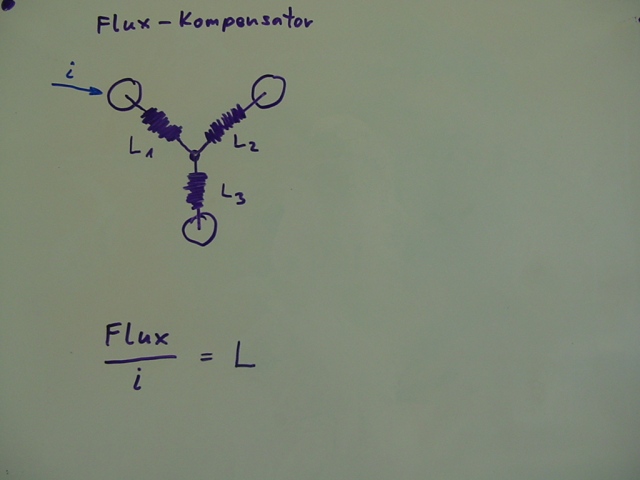
Für jedes einzelne Element des Flux-Kompensators – entsprechend L1, L2, L3 …

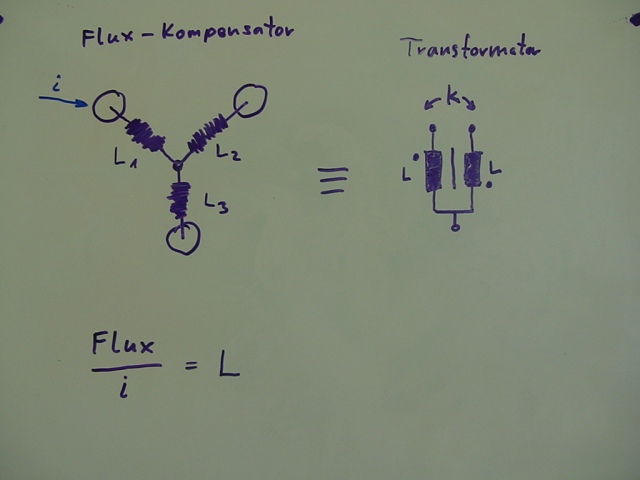
… und stellen verblüfft fest – der Flux-Kompensator ist identisch mit einem Transformator !

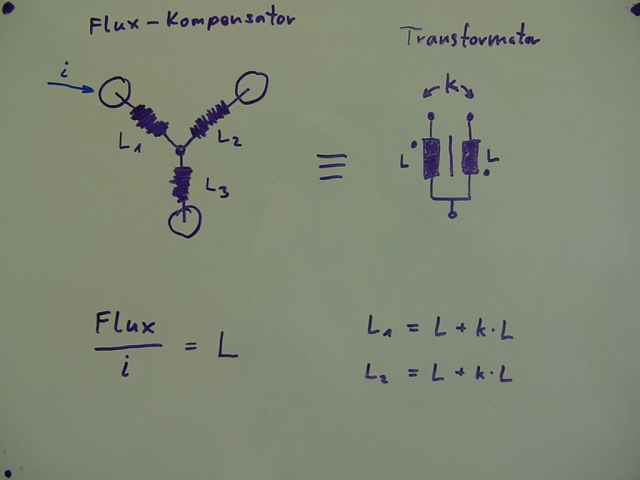
Wobei sich L1 und L2 entsprechend der Formeln umrechnen …

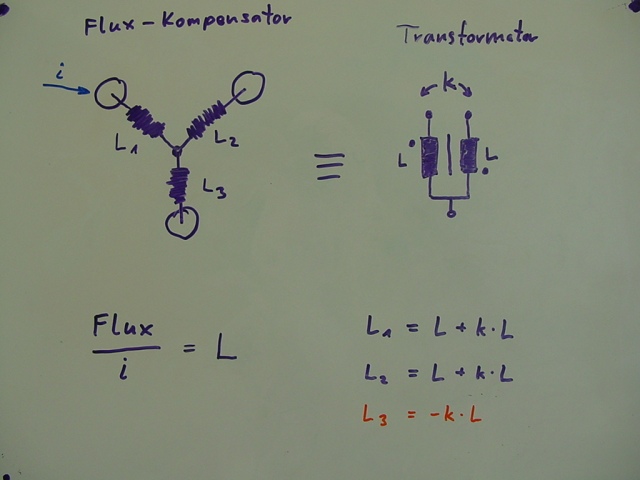
... und – das ist der Clou ! – L3 tatsächlich einen negativen Wert annimmt !

Wir haben also mit Hilfe einer Zeitmaschine eine passive, frequenzunabhängige

negative Induktivität erzeugt !

Glaubt ihr nicht ? Ist alles korrekt !

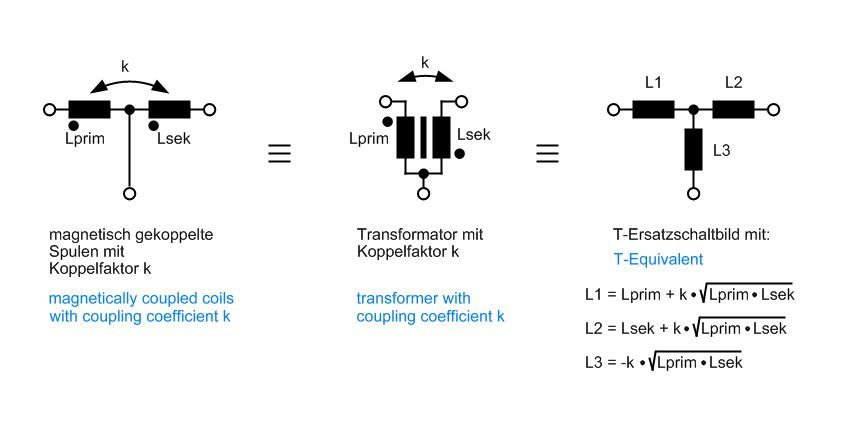
Und für die Experten – noch mal alle Formeln in der Zusammenstellung

.

.

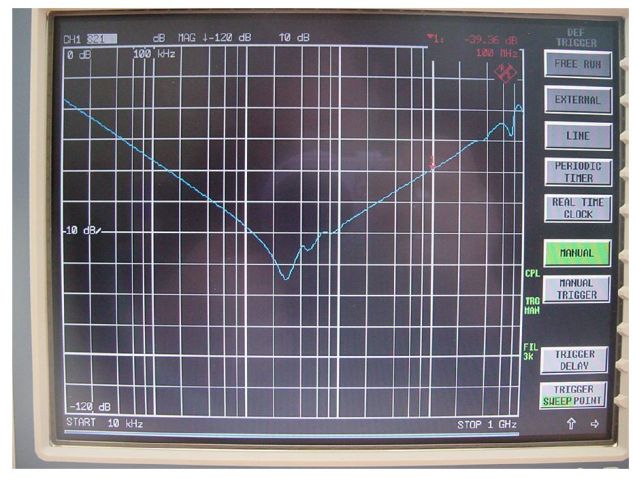
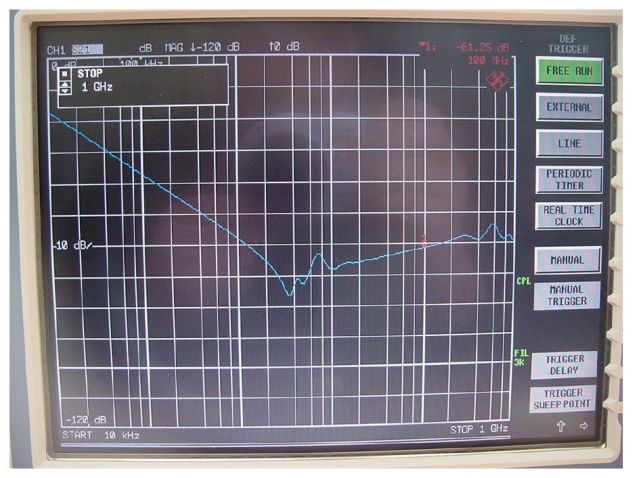
Und so sieht eine handgemachte negative Induktivität in echt aus :

Der Kondensator ist an den Mittelabgriff der Spule angelötet.

Die Windungsfläche (die Induktivität) und der Abstand zwischen den Windungen (die Kopplung)

ist so gewählt, daß sich am Verbindungspunkt zum Kondensator eine negative Induktivität ergibt,

die gerade so groß ist, wie die parasitäre Induktivität des Kondensators.

Wie man sich leicht vorstellen kann, ist das bei diesen Abmessungen von Hand ein ziemliches

Gefrickel – ganz exakt den richtigen Wert bekommt man nicht hin – mit ±10% Abweichung

muß man rechnen.

Aber auch so sind die Ergebnisse beeindruckend, verblüffend und faszinierend.

.

.

Normaler Kondensator

.

.

Kondensator zusammen mit der negativen Induktivität (siehe Foto oben)

.

.

Nachtrag

Diese Methode negative Induktivitäten zu erzeugen, war bis vor wenigen Jahren unbekannt – obwohl die

dahinter steckende Physik (Transformator) und die zugehörigen Formeln schon seit über 100 Jahren gelehrt

und angewendet wurden. Allerdings bekamen die Studierenden auf die Frage, was man denn machen solle,

wenn im Ersatzschaltbild negative Werte für die Bauteile herauskämen, regelmäßig die Antwort, das könne

man so nicht verwenden – weil es in der Realität keine negativen Bauteile gebe !

Und viele glauben das noch immer !(Klassische Interpretation von negativen Induktivitäten)

Tatsächlich ist es genau anders herum ! Wenn das Ersatzschaltbild ein negatives Bauteil liefert, verhält

sich die reale Schaltung so, als wäre ein negatives Bauteil tatsächlich vorhanden – auch wenn es

nicht sichtbar ist.

Weiterführende Erläuterungen unter – Filter mit Negativer Induktivität

.

Nur aus Spaß – einfach mal googeln – nach negative Induktivität (mit oder ohne Anführungszeichen)

und schauen, was da raus kommt !

.